Overview

A fundamental assumption in our current theories of the Universe is that photons always travel at the same speed, \(c\), independent of their energy. But this needs not be true. If the photon had a non-zero rest mass, then lower energy photons would travel slower (\(v < c\)). Alternatively, it is expected that quantum fluctuations of spacetime at high energies in so-called quantum gravity (QG) theories would make spacetime appear “foamy”, and thus empty space would have an energy-dependent refractive index. Or perhaps photons of different energy couple to gravity with different strengths (and thus violate the weak equivalence principle), so that photons of different energy travel differently through a gravitational field. In any one of these cases, photons of different energies from a distant source would arrive at different times, even if they were emitted simultaneously. Since the expected time delay increases with distance travelled, by studying the energy-dependent arrival times (spectral lag) of photons from sources at high redshift, we can place tight constraints on the quantum gravity length scale, \(\ell_{\rm QG}\), the photon mass, \(m_\gamma\), or the different couplings of photons to gravity at different energy, \(\Delta \gamma\). The high redshifts and short durations of Gamma Ray Bursts (GRBs) are ideal for this, so this is what we consider here. For the majority of Gamma Ray Burts, high energy photons are detected before lower energy photons, which is qualitatively the same as for a massive photon and some quantum gravity models, and could thus provide evidence for such theories.

The gravitational time delay

To constrain the equivalence principle, we must be able to predict how long it takes a photon to travel through a gravitational field. The resulting time delay to a distant source depends on the gravitational potential along the path that it travels and thus depends on the direction in the sky. If one had knowledge of the true present-day matter field, then one could create maps of the expected time delay as a function of source position. Indeed, in previous attempts to constrain equivalence-principle violation, \(\delta \phi\) was modelled as arising from one or a few isolated sources near the line of sight, however the long range of gravity casts doubt on the multiple point masses approximation. Instead, we account fully for the contributions to the time delay from all mass in the non-linear cosmological density field. We derive the contribution from local structures using constrained density fields generated by the BORG reconstruction of SDSS-III/BOSS ¹, and combine this with an unconstrained contribution from distant sources to produce a Monte-Carlo based source-by-source forward model for the expected time delay. The ensemble mean of the resulting time delay fluctuation map is plotted in Figure 1, and is \(\sim 10^{11} {\rm \, s}\) for a source at \(z=0.1\).

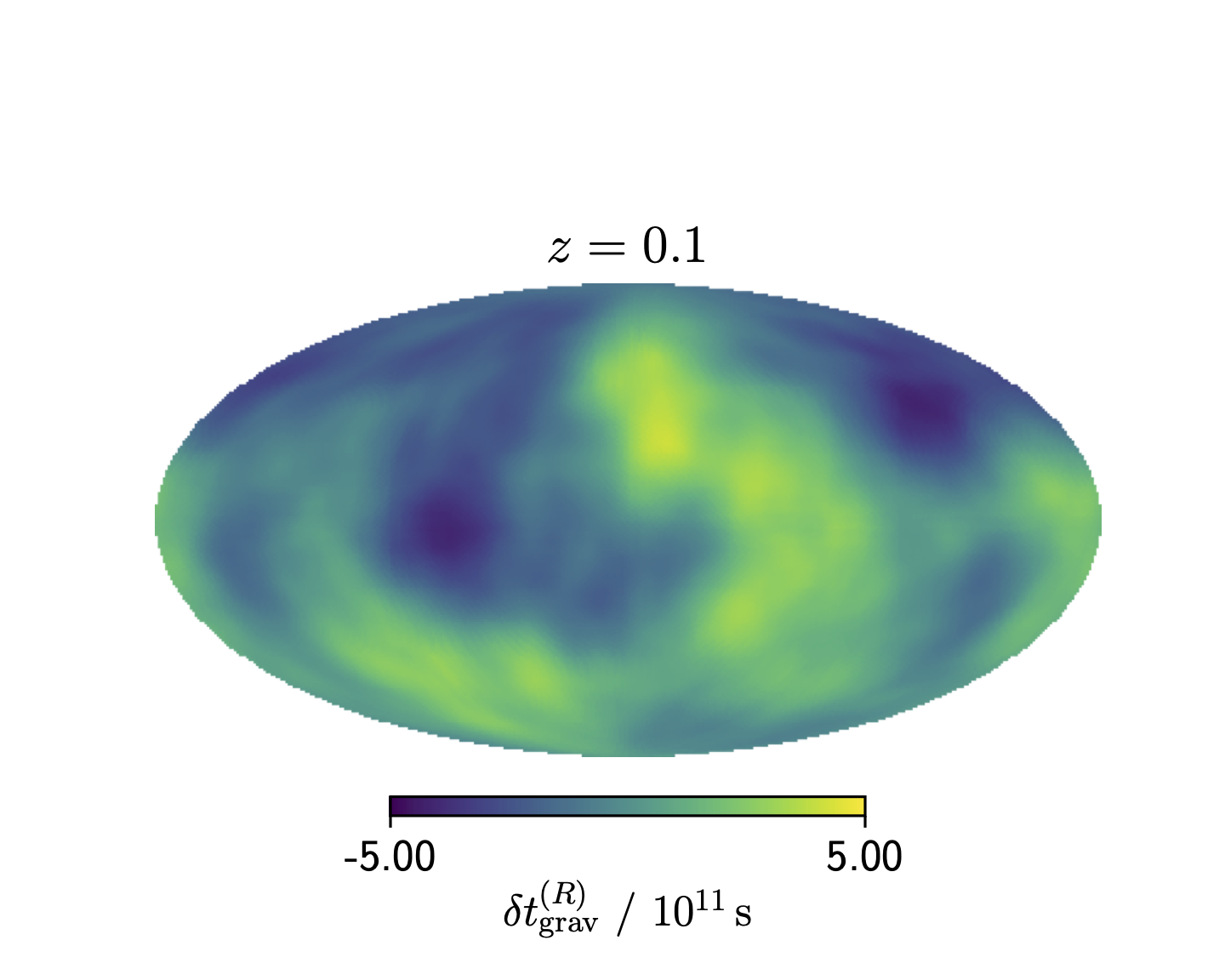Mollweide projection in equatorial coordinates of the ensemble mean of the time delay fluctuations at \(z=0.1\) from wavelengths resolved by the BORG reconstruction.

Forward modelling the time delays

We use a catalogue of 668 Gamma Ray Bursts for the BATSE satellite since these not only have spectral lag data, but also pseudoredshifts calculated using the spectral peak energy-peak luminosity relation. Propagating uncertainties on the pseudoredshifts, sky localisation and spectral parameters through Monte Carlo Sampling, we produce source-by-source forward models for the likelihood of a time delay from quantum gravity, a photon mass or equivalence principle violation. However, these are not the only types of physics that can lead to spectral lags: these may also be generated through intrinsic differences in the emission of photons of different wavelength at the source or their propagation through the medium surrounding the Gamma Ray Burst, or through instrumental effects at the observer. Without a robust physical model for the time delays these lead to, we model them using a generic functional form (a sum of Gaussians) with free parameters that we marginalise over in constraining \(m_\gamma\), \(\ell_{QG}\) and \(\Delta\gamma\). We vary the number of Gaussians used to describe these observational and astrophysical processes to find the best-fitting model to the data. Importantly, we find that our results are insensitive to this choice; a vital check that was often neglected in previous work. We compare our predicted time delays to the observed ones through a MCMC algorithm and therefore constrain \(m_\gamma\), \(\ell_{QG}\) and \(\Delta\gamma\).

Is the speed of light energy dependent?

We find no evidence that the speed of light has an energy dependence. We constrain the photon mass to be \(m_\gamma < 4.0 \times 10^{-5} \, h \, {\rm eV}/c^2\) and the quantum gravity length scale to be \(\ell_{\rm QG} < 5.3 \times 10^{-18} \, h \, {\rm \, GeV^{-1}}\) at 95% confidence ². As shown in Figure 2, the quantum gravity constraint is the tightest from time delay studies which consider multiple Gamma Ray Bursts, and the constraint on \(m_\gamma\), although weaker than from using radio data, provides an independent constraint which is less sensitive to the effects of dispersion by electrons. We also place upper limits on an energy dependence of \(\gamma\) of \(\Delta \gamma < 2.1 \times 10^{-15}\) at \(1 \sigma\) confidence between photon energies of \(25 {\rm \, keV}\) and \(325 {\rm \, keV}\) ³. These constraints are 40 times tighter than literature results, illustrating the benefits of using complete mass distributions when studying non-local relativistic effects such as time delays.

So what can we say about quantum gravity, the photon mass and the equivalence principle? Through the use of simulation based, Bayesian statistical forward-modelling techniques and the BORG algorithm, we have produced some of the tightest constraints on these theories to date, and have demonstrated that the results are robust to how one models other astrophysical and observational contributions to the observed signal. It is expected that \(\ell_{\rm QG}\) should be near the Planck length, which is approximately two orders of magnitude smaller than we are currently sensitive to, so we are yet to probe this. It is expected that detecting Gamma Ray Bursts at \(>100 {\rm \, GeV}\) should be routine in the future; with more, higher energy measurements one should begin to probe this energy scale, so there is the tantalising possibility of making the first detection of quantum gravity as these limits approach the Planck scale in the near future.

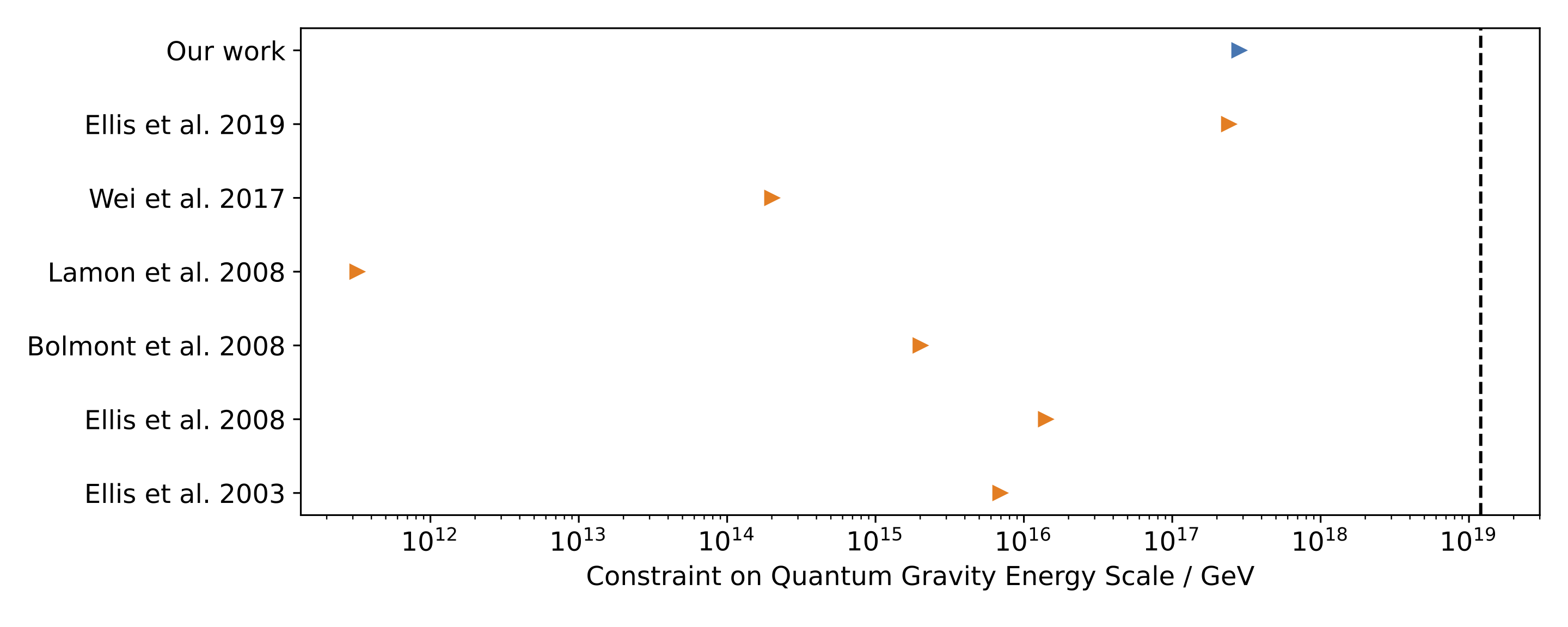Lower limits on the quantum gravity energy scale (\(1 / \ell_{\rm QG}\)) from time delay studies which use multiple astrophysical sources. Our work provides the tightest constraint to date. The dashed vertical line is the Planck energy, and it is expected that the quantum gravity energy scale has approximately this value.